Bilangan Bulat
Pengertian Bilangan BulatBilangan bulat adalah bilangan yang terdiri atas bilangan cacah ( 0,1,2,3,….) dan bilangan negatif dari bilangan tersebut(…,-3,-2,-1,-0), karena -0 sama dengan 0 maka cukup dituliskan satu kali. Sehingga bilangan bulat memiliki anggota dari -∞ hingga ∞ jika dituliskan adalah sebagai berikut :
…..,-2,-1,0,1,2,…..
Jika disajikan dalam garis bilangan :
Operasi Hitung Pada Bilangan Bulat
Operasi hitung yang ada pada bilangan bulat adalah operasi penjumlahan, pengurangan, perkalian dan pembagian.
Menaksir Hasil Perkalian Dan Pembagian Bilangan Bulat
Menaksir adalah proses membulatkan bilangan bulat.
Cara yang dilakukan untuk mencari hasil pembulatan atau taksiran adalah sebagai berikut.
- 1. Pembulatan ke angka puluhan terdekat.
- a. Jika angka satuannya kurang dari 5, angka tersebut tidak dihitung atau dihilangkan.
b. Jika angka satuannya lebih dari atau sama dengan 5, angka tersebut dibulatkan ke atas menjadi puluhan.
- 2. Pembulatan ke angka ratusan terdekat
- a. Jika angka puluhannya kurang dari 5, angka puluhan dan satuan dihilangkan.
b. Jika angka puluhannya lebih dari atau sama dengan 5, angka puluhan tersebut dibulatkan ke atas menjadi ratusan.
Kelipatan Dan Faktor
Sebelum membahas lebih dalam mengenai Kelipatan dan Faktor, ingat kembali apa itu bilangan prima, dan apa itu faktor.
Bilangan Prima adalah bilangan yang tepat mempunyai dua faktor, yaitu 1 dan dirinya sendiri.
Faktor dari suatu bilangan asli n adalah suatu bilangan asli yang apabila dikalikan dengan bilangan asli lain hasilnya sama dengan n.
Perpangkatan Bilangan Bulat
Perpangkatan suatu bilangan bulat adalah perkalian berulang dengan bilangan yang sama.
Operasi Hitung Campuran Pada Bilangan Bulat
Dalam menyelesaikan operasi hitung bilangan bulat, terdapat dua hal yang perlu kalian perhatikan, yaitu
- 1. tanda operasi hitung;
2. tanda kurung.
Apabila dalam suatu operasi hitung bilangan bulat tidak terdapat tanda kurung, pengerjaannya berdasarkan sifat-sifat operasi hitung berikut :
- 1. Operasi penjumlahan (+) dan
pengurangan (–) sama kuat, Artinya operasi yang terletak di sebelah kiri
dikerjakan terlebih dahulu.
2. Operasi perkalian (
3. Operasi perkalian (
Salam Matematika
AKAR DAN PANGKAT BILANGAN BULAT
AKAR DAN PANGKAT BILANGAN BULAT
 Akar dan pangkat bilangan bulat,
itulah yang akan kita pelajari pada postingan kali ini. Mudah-mudahan bisa
bermanfaat bagi teman-teman semua. Akar dan pangkat bilangan bulat ini memuat
bilangan pangkat dua, akar sederhana, dan contoh serta pembahasan akar dan
pangkat bilangan bulat itu sendiri.
Akar dan pangkat bilangan bulat,
itulah yang akan kita pelajari pada postingan kali ini. Mudah-mudahan bisa
bermanfaat bagi teman-teman semua. Akar dan pangkat bilangan bulat ini memuat
bilangan pangkat dua, akar sederhana, dan contoh serta pembahasan akar dan
pangkat bilangan bulat itu sendiri.
Selamat belajar dan penuh semangat
!!!
A.
Bilangan Pangkat Dua
Perkalian dengan dua bilangan yang sama
dapat ditulis dalam bentuk pangkat dua.
Contoh :
1 x 1 = 12
2 x 2 = 22
B.
Akar Sederhana
1.
Mengenal Akar Sederhana (akar pangkat dua)
2.
Menentukan akar pangkat dua ( akar
kuadrat)
Contoh :
Menentukan akar pangkat dua dari angka yang lebih besar dengan
cara :
a.
Pisahkan dua-dua angka dari kanan.
b.
Carilah nilai akar pangkat dua yang
hasilnya sama atau mendekati pemisahahn dua angka pertama. Kemudian kurangkan.
c.
Turunkan sisa pemisahan dua angka yang
lain.
d.
Jumlahkan bilangan pokok pada langkah
(b).
e.
Simpan suatu bilangan disamping langkah
ke (d). carilah hasil kalinya yang sama dengan sisa bilangan akar tadi.
Contoh :
·
Carilah nilai dari 
Jawab
Hasilnya adalah 13 yang diambil dari 1 dari 1 x 1 dan 3 dari 3 x
3, sehingga hasilnya adalah 13
·
Hitunglah nilai dari 
Jawab
Jadi, hasilnya adalah 123
C.
Contoh dan Pembahasan Akar dan Pangkat
Bilangan Bulat
1.
55 – 72 = 55 – 49
2.
126 + 12 x
 = 126 + 12 x 7
= 126 + 12 x 7
= 126 + 84
= 210
3.
122 – 102 : 5 = 144
– 100 : 5
= 144 – 20
= 124
4.
-150 – 152 : 32 = -150 – 225 : 9
= -150 – 25
= -150 + (-25)
= -175
5.
-16 : 22 + 27 : = -16 : 4 + 27 : 3
= -16 : 4 + 27 : 3
= -4 + 9
= 5
Untuk
mendapatkan nilai FPB dan KPK, langkah pertama adalah mencari
faktorisasi prima dari bilangan yang akan dicari nilai FPB atau KPK nya.
Faktorisasi prima adalah cara menyatakan bilangan dalam bentuk
perkalian bilangan-bilangan prima. Jadi, sobat idschool harus mengerti
apa itu bilangan prima terlebih dahulu.
Bilangan prima adalah bilangan asli lebih dari satu yang hanya dapat dibagi oleh 1 (satu) dan bilangan itu sendiri. Contoh bilangan prima adalah 13, bilangan 13 hanya bisa dibagi oleh 1 dan 13, tidak ada bilangan yang dapat membagi habis 13 selain 1 dan 13. Dengan demikian, bilangan 13 termasuk dalam bilangan prima. Daftar bilangan prima (P) lainnya adalah sebagai berikut.
![Rendered by QuickLaTeX.com \[ P = \left \{ 2, \; 3, \; 5, \; 7, \; 11, \; 13, \; ... \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-05822b5800f04696526039cab33b64f7_l3.png) Lawan
dari bilangan prima adalah bilangan komposit. Dalam kata lain, bilangan
komposit dapat dinyatakan sebagai bilangan asli lebih besar dari 1 yang
bukan merupakan bilangan prima. Daftar bilangan komposit (K) adalah
sebagai berikut.
Lawan
dari bilangan prima adalah bilangan komposit. Dalam kata lain, bilangan
komposit dapat dinyatakan sebagai bilangan asli lebih besar dari 1 yang
bukan merupakan bilangan prima. Daftar bilangan komposit (K) adalah
sebagai berikut.
![Rendered by QuickLaTeX.com \[ K = \left \{ 4, \; 6, \; 8, \; 9, \; 10, \; 12, \; ... \right \}\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ef6c3925eef2cfe9f0fabb02692e82c9_l3.png) Setelah
menentukan semua faktorisasi prima dari bilangan yang akan dicari KPK
dan FPB nya, sobat idschool dapat menentukan nilai KPK dan FPB nya.
Nilai FPB diperoleh dari perkalian semua faktor prima yang sama dengan
pangkat terkecil. Sedangkan nilai KPK diperoleh dari perkalian semua
faktor prima dengan pangkat terbesar. Ini adalah cara yang biasanya
diberikan di sekolah.
Setelah
menentukan semua faktorisasi prima dari bilangan yang akan dicari KPK
dan FPB nya, sobat idschool dapat menentukan nilai KPK dan FPB nya.
Nilai FPB diperoleh dari perkalian semua faktor prima yang sama dengan
pangkat terkecil. Sedangkan nilai KPK diperoleh dari perkalian semua
faktor prima dengan pangkat terbesar. Ini adalah cara yang biasanya
diberikan di sekolah.
Sebenarnya ada cara cepat mencari FPB dan KPK, cara tersebut dinamakan petak sawah, karena bentuknya berupa petak-petak. Denagn cara patak sawah, sobat idschool tidak perlu mencari faktorisasi prima terlebih dahulu. Ulasan materi yang akan dibahas di bawah adalah penjelasan lebih detail mengenai cara mencari FPB dan KPK. Selain itu, akan diulas juga cara cepat mencari FPB dan KPK menggunakan cara petak sawah. Jadi, simak sampai akhir pembahasan, oke!
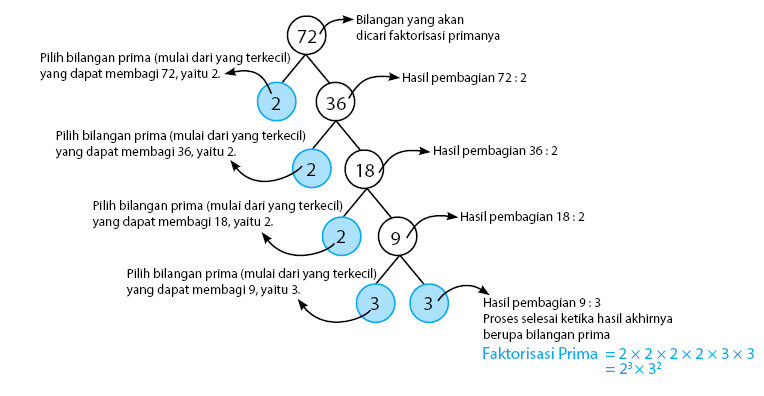
Berdasarkan hasil perhitungan di atas dapat diperoleh faktorisasi prima dari bilangan 72 adalah
![Rendered by QuickLaTeX.com \[ 72 = 2^{3} \times 3^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0d5c5ef39ef24de2d334c82fa23260e7_l3.png) Berikutnya akan diulas cara mencari FPB dan KPK dan cara cepatnya. Simak penjelasan lebih lanjut pada uraian materi di bawah.
Berikutnya akan diulas cara mencari FPB dan KPK dan cara cepatnya. Simak penjelasan lebih lanjut pada uraian materi di bawah.
Faktorisasi prima dari 24:
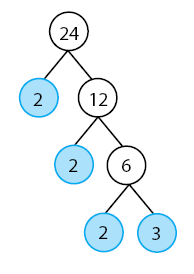
Sehingga,
![Rendered by QuickLaTeX.com \[ 24 = 2^{3} \times 3 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-cf5c03f751e3623315f1648baefcbccd_l3.png) Faktorisasi prima dari 81:
Faktorisasi prima dari 81:
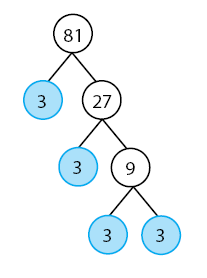
Sehingga,
![Rendered by QuickLaTeX.com \[ 81 = 3^{4} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d6ea318d5015fc64ebeb1b95b269ca34_l3.png) Faktorisasi prima dari 108:
Faktorisasi prima dari 108:
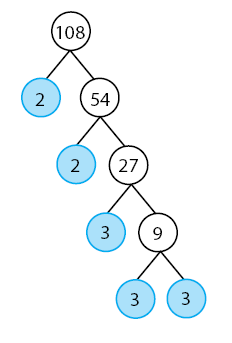
![Rendered by QuickLaTeX.com \[ 108 = 2^{2} \times 3^{3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c2ec92146ec4b45ce3df1f585b5e2727_l3.png) Daftar faktorisasi ketiga bilangan prima ditulis ulang seperti berikut ini.
Daftar faktorisasi ketiga bilangan prima ditulis ulang seperti berikut ini.
![Rendered by QuickLaTeX.com \[ 24 = 2^{3} \times 3 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-cf5c03f751e3623315f1648baefcbccd_l3.png)
![Rendered by QuickLaTeX.com \[ 81 = 3^{4} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d6ea318d5015fc64ebeb1b95b269ca34_l3.png)
![Rendered by QuickLaTeX.com \[ 108 = 2^{2} \times 3^{3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c2ec92146ec4b45ce3df1f585b5e2727_l3.png) Nilai FPB diperoleh dari perkalian semua faktor prima yang sama dengan pangkat terkecil.
Nilai FPB diperoleh dari perkalian semua faktor prima yang sama dengan pangkat terkecil.
![Rendered by QuickLaTeX.com \[ FPB = 3 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ef69fe35aef5f6a81d6e1f025f0f6730_l3.png) Nilai KPK diperoleh dari perkalian semua faktor prima dengan pangkat terbesar.
Nilai KPK diperoleh dari perkalian semua faktor prima dengan pangkat terbesar.
![Rendered by QuickLaTeX.com \[ KPK = 2^{3} \times 3^{4} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-cf72ee7022ab70e29df8a2f60de40f98_l3.png)
![Rendered by QuickLaTeX.com \[ KPK = 8 \times 81 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-719e4297fee3310d1c2c68bc324304d4_l3.png)
![Rendered by QuickLaTeX.com \[ KPK = 648 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c735e556b7dff64f9e0ab0377d4cb088_l3.png) Demikianlah
cara mencari FPB dan KPK dengan cara runut. Selanjutnya, sobat idschool
akan menyimak cara cepat menentukan FPB dan KPK, yaitu cara petak
sawah.
Demikianlah
cara mencari FPB dan KPK dengan cara runut. Selanjutnya, sobat idschool
akan menyimak cara cepat menentukan FPB dan KPK, yaitu cara petak
sawah.
Mencari FPB dengan cara petak sawah diperoleh dengan membagi habis bilangan-bilangan yang akan dicari nilai FPB nya dengan bilangan prima, biasanya dimulai dari yang terkecil. Prosesnya berhenti ketika tidak ada bilangan prima lagi yang dapat membagi habis bilangan-bilangan yang akan dicari nilai FPB nya. Hasil FPB nya adalah perkalian bilangan prima yang dapat membagi habis bilangan-bilangan yang akan dicari nilai FPB nya. Perhatikan cara mencari nilai FBP untuk bilangan 24, 81, dan 108 di bawah.
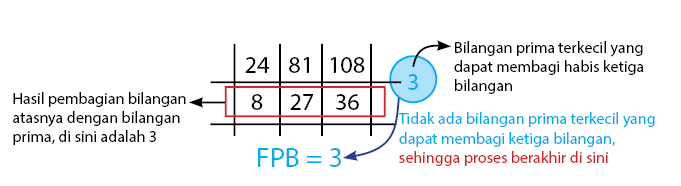
Diperoleh hasil FPB dari 24, 81, dan 108 adalah 3.
Mencari KPK dengan cara petak sawah diperoleh dengan membagi habis bilangan-bilangan yang akan dicari nilai KPK nya dengan bilangan prima, biasanya dimulai dari yang terkecil. Jika ada bilangan yang tidak bisa dibagi habis oleh suatu bilangan prima maka nilainya tetap. Prosesnya berakhir ketika hasil akhir semuanya adalah 1 (satu). Perhatikan cara mencari nilai KPK untuk bilangan 24, 81, dan 108 di bawah.
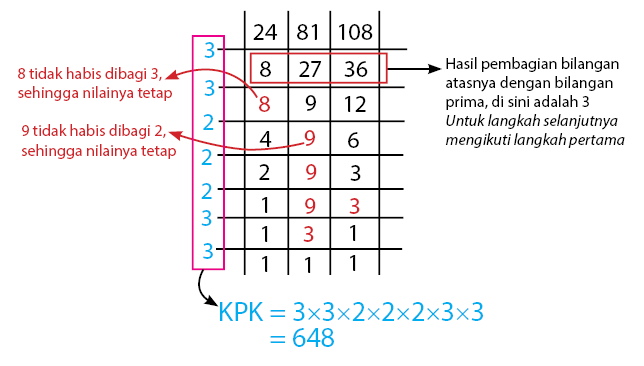
Diperoleh hasil KPK dari 24, 81, dan 108 adalah 648.
Nilai FPB dan KPK dengan cara faktorisasi prima dan petak sawah adalah sama, bukan? Selanjutnya akan diberikan contoh soal penerapan FPB dan KPK dalam kehidupan sehari-hari. Jenis soal ini sering keluar dalam ujian nasional. Jadi, simak contoh soal FPB dan KPK yang diberikan di bawah.
Toko Sembako dikunjungi pemasok telur setiap 8 hari sekali, pemasok sabun setiap 15 hari sekali, dan pemasok mie setiap 30 hari sekali. Jika tanggal 2 November 2014 ketiga pemasok datang bersama, maka mereka akan datang bersama lagi pada tanggal ….
A. 4 Maret 2015
B. 3 Maret 2015
C. 2 Maret 2015
D. 1 Maret 2015
Pembahasan:
Langkah pertama adalah mencari nilai KPK dari 8, 15, dan 30. Akan digunakan cara petak sawah.
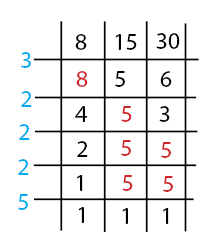
![Rendered by QuickLaTeX.com \[ KPK = 3 \times 2^{3} \times 5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3d23e84348614f5acc22f6abf4bdee43_l3.png)
![Rendered by QuickLaTeX.com \[ KPK = 120 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-97dcbcf88ab109eccabb23c32504f507_l3.png) Mencari
tanggal 120 hari setelah 2 November 2014. Proses perhitungan maju
setelah 2 November 2014 sejumlah 120 hari adalah sebagai berikut.
Mencari
tanggal 120 hari setelah 2 November 2014. Proses perhitungan maju
setelah 2 November 2014 sejumlah 120 hari adalah sebagai berikut.
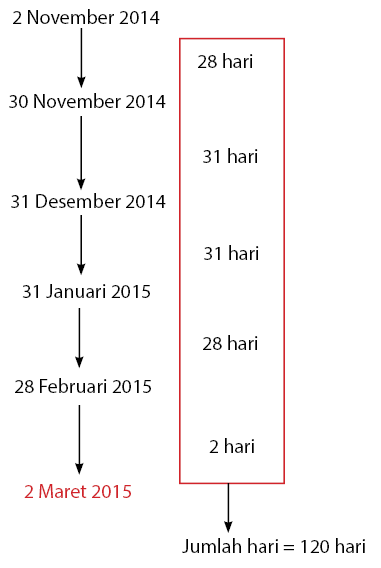
Jadi, ketiga pemasok datang bersama lagi pada tanggal 2 Maret 2015.
Jawaban: C
Contoh Soal FPB dan KPK 2
Ibu membeli 4 lusin pensil dan 3 lusin buku gambar. Ibu akan membagi pensil dan buku gambar kepada sejumlah anak paling banyak secara merata. Banyak pensil yang akan diterima setiap anak adalah ….
A. 6
B. 5
C. 4
D. 3
Pembahasan:
Banyaknya pensil = 4 lusin = 4 x 12 buah = 48 buah pensil.
Banyaknya buku gambar = 3 lusin = 3 x 12 = 36 buah buku gambar.
Mencari nilai FPB dari 48 dan 36:
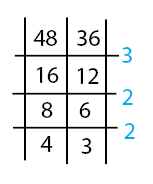
![Rendered by QuickLaTeX.com \[ KPK = 3 \times 2^{2} = 3 \times 4 = 12 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-c8178847ccbbef9f00defd71874d46ca_l3.png) Kesimpulannya, pensil dan buku gambar akan dibagikan kepada 12 anak. Banyaknya pensil yang diperoleh setiap anak adalah
Kesimpulannya, pensil dan buku gambar akan dibagikan kepada 12 anak. Banyaknya pensil yang diperoleh setiap anak adalah
![Rendered by QuickLaTeX.com \[ = \frac{48}{12} = 4 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-bf76a6999ce2ed1c8fcd9e37773de47e_l3.png) Jawaban: D
Jawaban: D
Cara Cepat Mencari FPB dan KPK
Bilangan prima adalah bilangan asli lebih dari satu yang hanya dapat dibagi oleh 1 (satu) dan bilangan itu sendiri. Contoh bilangan prima adalah 13, bilangan 13 hanya bisa dibagi oleh 1 dan 13, tidak ada bilangan yang dapat membagi habis 13 selain 1 dan 13. Dengan demikian, bilangan 13 termasuk dalam bilangan prima. Daftar bilangan prima (P) lainnya adalah sebagai berikut.
Sebenarnya ada cara cepat mencari FPB dan KPK, cara tersebut dinamakan petak sawah, karena bentuknya berupa petak-petak. Denagn cara patak sawah, sobat idschool tidak perlu mencari faktorisasi prima terlebih dahulu. Ulasan materi yang akan dibahas di bawah adalah penjelasan lebih detail mengenai cara mencari FPB dan KPK. Selain itu, akan diulas juga cara cepat mencari FPB dan KPK menggunakan cara petak sawah. Jadi, simak sampai akhir pembahasan, oke!
Faktorisasi Prima
Sebelum belajar mencari nilai FPB dan KPK, akan diulas terlebih dahulu cara mencari faktorisasi prima dari suatu bilangan. Pada pembahasan kali ini, bilangan yang akan dicari faktorisasi primanya adalah 72. Simak cara mencari faktorisasi prima dari bilangan 72 yang akan diberikan di bawah.
Berdasarkan hasil perhitungan di atas dapat diperoleh faktorisasi prima dari bilangan 72 adalah
Mencari FPB dan KPK dengan Cara Runut
Dalam pembahasan di sini, akan diberikan cara umum untuk menentukan nilai FPB dari tiga bilangan. Misalnya, bilangan yang akan dicari nilai FPB nya adalah 24, 81, dan 108. Langkah pertama, kita akan menentukan faktorisasi prima dari ketiga bilangan tersebut.Faktorisasi prima dari 24:

Sehingga,

Sehingga,

Mencari FPB dan KPK dengan Cara Cepat (Cara Petak Sawah)
Sebelumnya, sudah diuraikan cara menentukan FPB dan KPK dengan cara runut. Melalui pembahasan di sini akan diuraikan cara menentukan FPB dan KPK dengan cara cepat, yaitu cara petak sawah. Agar dapat membadingkan hasilnya, akan dicari nilai FPB dan KPK untuk tiga bilangan yang telah dicari nilai FPB dan KPK sebelumnya, yaitu 24, 81, dan 108.Mencari FPB dengan cara petak sawah diperoleh dengan membagi habis bilangan-bilangan yang akan dicari nilai FPB nya dengan bilangan prima, biasanya dimulai dari yang terkecil. Prosesnya berhenti ketika tidak ada bilangan prima lagi yang dapat membagi habis bilangan-bilangan yang akan dicari nilai FPB nya. Hasil FPB nya adalah perkalian bilangan prima yang dapat membagi habis bilangan-bilangan yang akan dicari nilai FPB nya. Perhatikan cara mencari nilai FBP untuk bilangan 24, 81, dan 108 di bawah.

Diperoleh hasil FPB dari 24, 81, dan 108 adalah 3.
Mencari KPK dengan cara petak sawah diperoleh dengan membagi habis bilangan-bilangan yang akan dicari nilai KPK nya dengan bilangan prima, biasanya dimulai dari yang terkecil. Jika ada bilangan yang tidak bisa dibagi habis oleh suatu bilangan prima maka nilainya tetap. Prosesnya berakhir ketika hasil akhir semuanya adalah 1 (satu). Perhatikan cara mencari nilai KPK untuk bilangan 24, 81, dan 108 di bawah.

Diperoleh hasil KPK dari 24, 81, dan 108 adalah 648.
Nilai FPB dan KPK dengan cara faktorisasi prima dan petak sawah adalah sama, bukan? Selanjutnya akan diberikan contoh soal penerapan FPB dan KPK dalam kehidupan sehari-hari. Jenis soal ini sering keluar dalam ujian nasional. Jadi, simak contoh soal FPB dan KPK yang diberikan di bawah.
Contoh Soal dan Pembahasan
Contoh Soal FPB dan KPK 1Toko Sembako dikunjungi pemasok telur setiap 8 hari sekali, pemasok sabun setiap 15 hari sekali, dan pemasok mie setiap 30 hari sekali. Jika tanggal 2 November 2014 ketiga pemasok datang bersama, maka mereka akan datang bersama lagi pada tanggal ….
A. 4 Maret 2015
B. 3 Maret 2015
C. 2 Maret 2015
D. 1 Maret 2015
Pembahasan:


Jadi, ketiga pemasok datang bersama lagi pada tanggal 2 Maret 2015.
Jawaban: C
Contoh Soal FPB dan KPK 2
Ibu membeli 4 lusin pensil dan 3 lusin buku gambar. Ibu akan membagi pensil dan buku gambar kepada sejumlah anak paling banyak secara merata. Banyak pensil yang akan diterima setiap anak adalah ….
A. 6
B. 5
C. 4
D. 3
Pembahasan:
Banyaknya pensil = 4 lusin = 4 x 12 buah = 48 buah pensil.
Banyaknya buku gambar = 3 lusin = 3 x 12 = 36 buah buku gambar.
Mencari nilai FPB dari 48 dan 36:







Tidak ada komentar:
Posting Komentar